Random select bit set
You can use “Select the bit position“ function from the Bit Twiddling Hacks page to select random set bit efficiently. - SO
std::bitset<32> word(0x1028);
unsigned long ulWord = word.to_ulong(); // ulWord == 0x1028
unsigned int bitcnt = word.count();
unsigned int randomSetBitIndex = 63-selectBit(ulWord, random() % bitcnt + 1);
unsigned long randomSetBit = 1 << randomSetBitIndex;Select the bit position (from the most-significant bit) with the given count (rank)
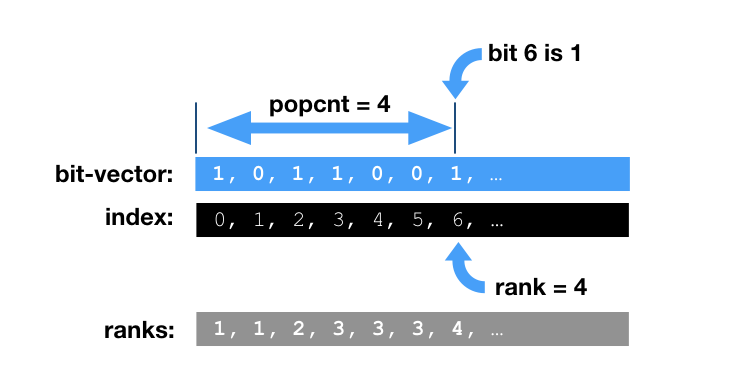
The following 64-bit code selects the position of the rth 1 bit when counting from the left. In other words if we start at the most significant bit and proceed to the right, counting the number of bits set to 1 until we reach the desired rank, r, then the position where we stop is returned. If the rank requested exceeds the count of bits set, then 64 is returned. The code may be modified for 32-bit or counting from the right.
uint64_t v; // Input value to find position with rank r.
unsigned int r; // Input: bit's desired rank [1-64].
unsigned int s; // Output: Resulting position of bit with rank r [1-64]
uint64_t a, b, c, d; // Intermediate temporaries for bit count.
unsigned int t; // Bit count temporary.Do a normal parallel bit count for a 64-bit integer, but store all intermediate steps.
a = v - ((v >> 1) & ~0UL/3); // a = (v & 0x5555...) + ((v >> 1) & 0x5555...);
b = (a & ~0UL/5) + ((a >> 2) & ~0UL/5); // b = (a & 0x3333...) + ((a >> 2) & 0x3333...);
c = (b + (b >> 4)) & ~0UL/0x11; // c = (b & 0x0f0f...) + ((b >> 4) & 0x0f0f...);
d = (c + (c >> 8)) & ~0UL/0x101; // d = (c & 0x00ff...) + ((c >> 8) & 0x00ff...);
t = (d >> 32) + (d >> 48);Now do branchless select!
s = 64;
// if (r > t) {s -= 32; r -= t;}
s -= ((t - r) & 256) >> 3; r -= (t & ((t - r) >> 8));
t = (d >> (s - 16)) & 0xff;
// if (r > t) {s -= 16; r -= t;}
s -= ((t - r) & 256) >> 4; r -= (t & ((t - r) >> 8));
t = (c >> (s - 8)) & 0xf;
// if (r > t) {s -= 8; r -= t;}
s -= ((t - r) & 256) >> 5; r -= (t & ((t - r) >> 8));
t = (b >> (s - 4)) & 0x7;
// if (r > t) {s -= 4; r -= t;}
s -= ((t - r) & 256) >> 6; r -= (t & ((t - r) >> 8));
t = (a >> (s - 2)) & 0x3;
// if (r > t) {s -= 2; r -= t;}
s -= ((t - r) & 256) >> 7; r -= (t & ((t - r) >> 8));
t = (v >> (s - 1)) & 0x1;
// if (r > t) s--;
s -= ((t - r) & 256) >> 8;
s = 65 - s;If branching is fast on your target CPU, consider uncommenting the if-statements and commenting the lines that follow them.
Notes
see popcount for explanation of bit count algorithm.
~0UL/3 == 0x5555555555555555
~0UL/5 == 0x3333333333333333
~0UL/0x11 == 0x0f0f0f0f0f0f0f0f
~0UL/0x101 == 0x00ff00ff00ff00ff