it refers to simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively. Likewise, in computer science, if a problem can be solved optimally by breaking it into sub-problems and then recursively finding the optimal solutions to the sub-problems, then it is said to have optimal substructure. - Wikipedia

Wilson was Secretary of Defense, and he actually had a pathological fear and hatred of the word “research” … dynamic programming was a good name. It was something not even a Congressman could object to. So I used it as an umbrella for my activities. - How Bellman came up with this name

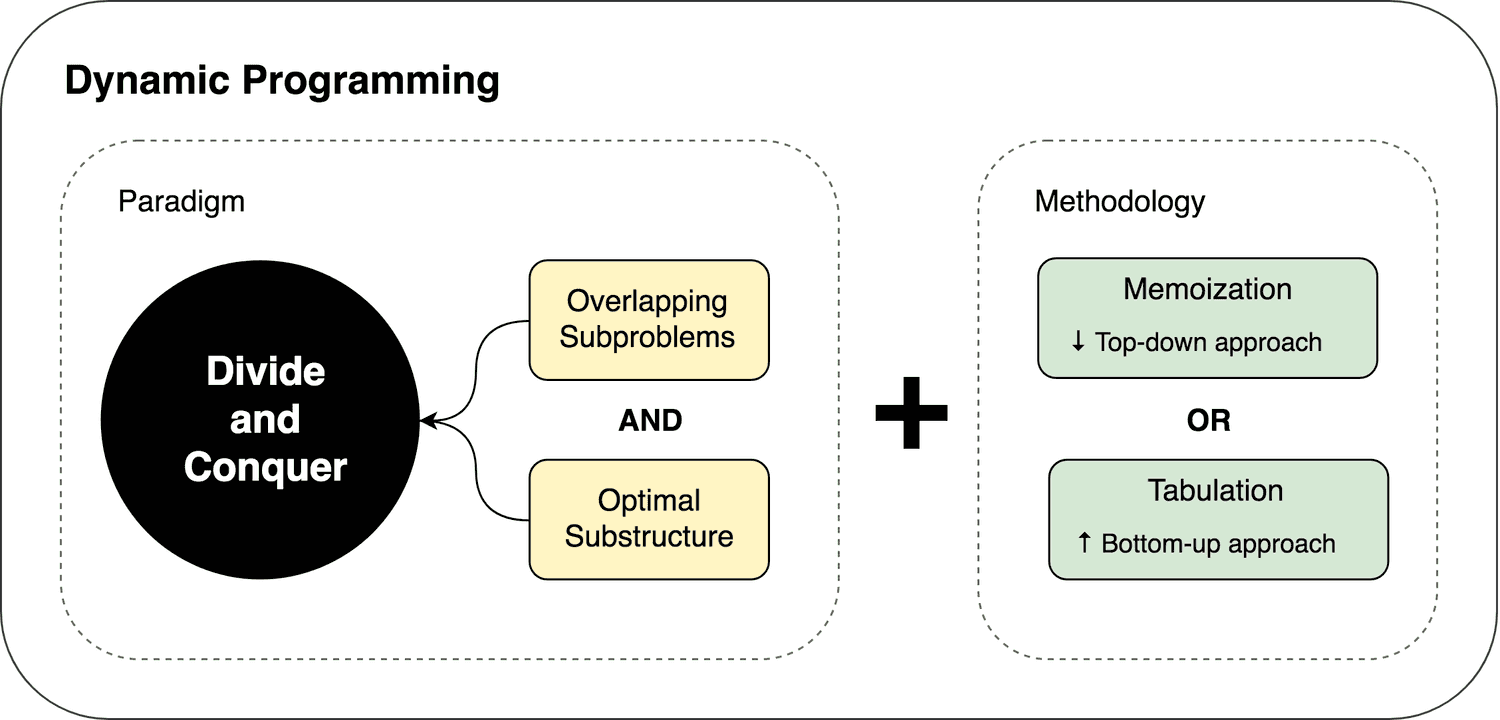
Dynamic Programming vs. Divide-and-Conquer (2018)

Learn to Solve Algorithmic Problems & Coding Challenges - youtube (5h)

• Memoisation / summary
  • fib memoization - from $O(2^n)$ to $O(n)$
  • gridTraveler memoization - problem decomposition into recursive then memoisation - from $O(2^{n+m})$ to $O(n*m)$
  • canSum memoization - can the combination of member of an array give the given sum. - from $O(n^m)$ to $O(n*m)$
    • howSum - generate one solution - from $O(n^m * m)$ to $O(n*m^2)$ with $O(m^2)$ space
    • bestSum - return minimum array
  • canConstruct memoization - word construction by concatenation from dictionnary (howSum with strings)
    • countConstruct - count the number of solution
    • allConstruct - give all solutions
• Tabulation
  • fib tabulation - generative iteration vs recursion: tree structure encoded in an array. - $O(n)$
  • gridTraveler tabulation - counting problem
• Sliding Window - a subset of dynamic programming problems

See also

• Breaking Down Dynamic Programming