Monte Carlo Tree Search was introduced by Rémi Coulom in 2006 as a building block of Crazy Stone – Go playing engine with an impressive performance. - Beginners guide

Monte Carlo Tree Search has one main purpose: given a game state to choose the most promising next move.

A game tree is a tree in which every node represents certain state of the game. Transition from a node to one of its children (if they exist) is a move. The number of node’s children is called a branching factor. Root node of the tree represents the initial state of the game. We also distinguish terminal nodes of the game tree – nodes with no children, from where game cannot be continued anymore. The terminal node’s states can be evaluated – this is where game result is concluded.

Upper Confidence Bounds for Trees (UCT)

$uct = \Large\frac{score}{visit} + C \sqrt{ \Large\frac{2*ln(V)}{visit} }$

Evaluation function using UCT is balanced between:

• exploration (second term) - meaning exploring tree space to gain new knowledge
• exploitation (first term - score) - meaning using aquired knowledge to focus on promising node.

As each node is visited, the denominator of the exploration term increases, which decreases its contribution. On the other hand, if another child of the parent node is visited, the numerator increases and hence the exploration values of unvisited siblings increase. The exploration term ensures that each child has a non-zero probability of selection, which is essential giventhe random nature of the playouts.

MCTS Algorithm

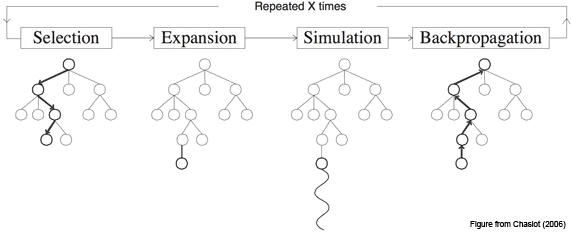
Monte-Carlo Tree search is made up of four distinct operations 1:
Selection - Start at the root node, and successively select a child until we reach a node that is not fully expanded.
Expansion - Unless the node we end up at is a terminating state, expand the children of the selected node by choosing an action and creating new nodes using the action outcomes.
Simulation - Choose one of the new nodes and perform a random simulation of the MDP to the terminating state.
Backpropagation - Given the reward $r$ at the terminating state, backpropagate the reward to calculate the value $V(s$ at each state along the path.

Pseudo Code

python code

code from Paper A Survey of Monte Carlo Tree Search Methods.

function UCTSEARCH(s0)
    create root node v0 with state s0
    while within computation budget dovl
        vl ← TREEPOLICY(v0)
        ∆  ← DEFAULTPOLICY(s(vl))
        BACKUP(vl,∆)
    return a(BESTCHILD(v0,0))

function TREEPOLICY(v)
    while v is nonterminal do
        if v not fully expanded then
           return EXPAND(v)
        else 
           v ← BESTCHILD(v,Cp)
    return v
    
function BACKUP(v,∆)
    while v is not null do
        N(v) ← N(v) + 1
        Q(v) ← Q(v) + ∆(v,p)
        v ← parent of v

Introduction

Basics

• Monte-Carlo Tree Search
• Introduction to Monte Carlo Tree Search

heavy rollout

• Integrating Monte Carlo Tree Search and Neural Networks
• Beyond Monte Carlo Tree Search: Playing Go withDeep Alternative Neural Network and Long-Term Evaluation

see also HN

Tic-Tac-Toe

Deep Dive

This essay digs into the “how do you reach a higher level of gameplay?” part of the process. Despite replacing all human heuristics, AlphaGoZero still uses tree search algorithms at its core. I hope to convince you that AlphaGoZero’s success is as much due to this algorithm as it is due to machine learning.

Good Explaination

Papers

• A Survey of Monte Carlo Tree Search Methods
• MCTS for multiplayer games
• Mastering the game of Go with deep neural networks and tree search
• Single-Player Monte-Carlo Tree Search