This suffers from CPU branch-prediction misses and extra overhead. But since our goal was to collect all of the nodes at the ideal resolutions for any given 3D view, non-recursive traversal is a bigger win. - Was Google Earth Stolen? / HN

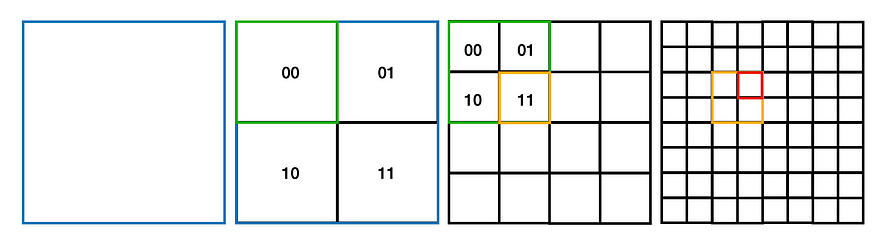
Quad-trees were invented in the 1970s (maybe 1966 if you consider morton-codes). The idea is to subdivide a large map or image into 4 equal tiles, recursively. Each tile or “node” also gets subdivided into 4, repeating as needed. As you zoom into the planet, you begin with the “root node” or main tile, and then the algorithm finds smaller tiles with effectively higher and higher resolution as needed. A typical quad-tree for the first four “levels.” Google Earth had 26+ levels.

Clip-mapping and Universal Texture both assume quad-tree subdivision of the source data, as do many other common uses, like storing roads and labels. I came up with a few optimizations that improved efficiency. The traditional “recursive descent” approach visits one node at a time, asking questions like “is this to the left, right, top, bottom, of some dividing lines?”

This suffers from CPU branch-prediction misses and extra overhead. But since our goal was to collect all of the nodes at the ideal resolutions for any given 3D view, non-recursive traversal is a bigger win.

The “addressing scheme”

the simplest approach.

Each quad node has four child nodes, named 0, 1, 2, 3 which is 00, 01, 10, 11 in binary. So the “address” of any given tile is just the string of these codes from the root down to the smallest child. Knowing that the first binary bit means up/down and the second means left/right allows the software to know the exact position and boundaries in space of any address, given only this string of bits (we might have reversed X and Y). It’s clever, efficient, but also not patent-worthy. It’s basically like morton codes, but intentionally sparse.