The Myth of RAM

Accessing memory is not a O(1) operation but O(√N). This is a result that holds up both in theory and practice. - ilikebigbits / HN

Let’s start with the latter:

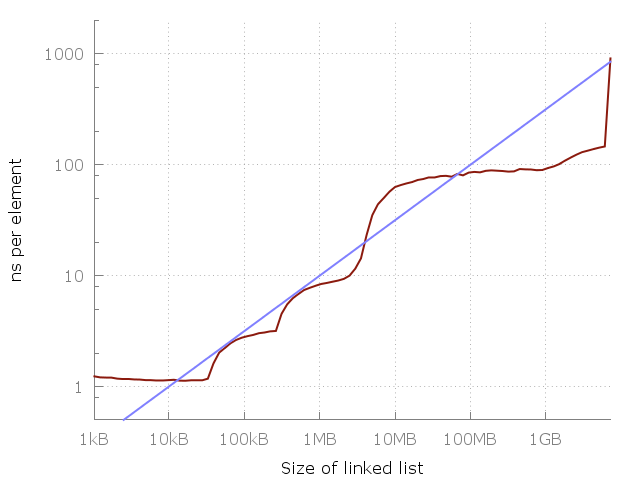
Here’s a simple program that iterates through a linked list of length N, ranging from 64 elements up to about 420 million elements. Each node consists of a 64 bit pointer and 64 bits of dummy data. The nodes of the linked list are jumbled around in memory so that each memory access is random. I measure iterating through the same list a few times, and then plot the time taken per element. This means that we should get a flat plot if random memory access is O(1). This is what we actually get:

The cost of accessing one node in a linked list of a given size. Accessing a random element in a 100MB list is approximately 100 times slower than accessing an element in a 10kB list.

The blue line corresponds to a O(√N) cost of each memory access. Seems like a pretty good fit, no? Of course this is on my machine, and it may look quite different on yours. Still, the equation is very simple to remember, so maybe we could use it as a rule of thumb.