Catching the rabbit (interception)

Given the coordinates of the positions of Alice, the rabbit and the hole, as well as the respective speeds of Alice and the rabbit, say whether Alice can catch the rabbit before it disappears. - Interception of a Linear Trajectory With Constant Speed

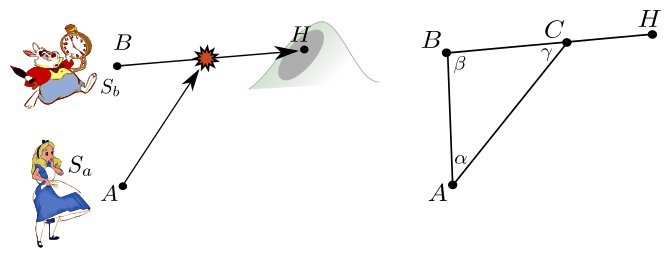
It is straightforward that, since we are looking for the fastest catch, Alice’s trajectory towards C must be a straight line.

caption

I had to solve the same problem at some point, and worked out this quadratic equation that solved it

My interpretation

Instead of previous model, consider that we collide at a time $t$. With $\vec{v_A}$ and $\vec{v_B}$ being respective speed vectors of $A$ and $B$, we got:

$A + t \vec{v_A}= B + t \vec{v_B} = C$ the point of collision (1).

Everything is known, except $t$ and $\vec{v_A}$ for which we know only the norm (= the speed), but not the direction.

The distance (the value) to the point of collision is equal to $t | \vec{v_A} |$ from $A$ and $t | \vec{v_B} |$ from B. That is time multiplied by the relative linear speed of the object.

What we have is a general triangle ABC, for which:

  • $\vec{AB}$ is known by definition,
  • $\vec{BC(t)} = t \vec{v_B} $ is dependant of $t$,
  • $AC(t) = t | \vec{v_A} | = t . s_A$ is a distance dependant of $t$.

We can use the vector version of Law of cosinus. Starting from the vector relation:

$\vec{AC}=\vec{AB} + \vec{BC}$

Taking the dot product of each side with itself, we got:

${AC(t)}^2 = {AB}² + {BC(t)}² + 2 \vec{AB}.\vec{BC(t)}$ where now everything is known except $t$.

which by replacing known quantities, become:

${(\boldsymbol t . s_A)}² = {AB}² + {(\boldsymbol t . s_B)}² + 2 \boldsymbol t . \vec{AB}.\vec{v_B}$

or

$ ({s_B}² - {s_A}²) \boldsymbol t² + ( 2 \vec{AB}.\vec{v_B}) \boldsymbol t + {AB}² = 0 $, a quadratic equation in $\boldsymbol t$ that we can now solve.

Then if a solution exist, it can be injected in (1) to compute $C$.

Interception within a range $d$

Let’s assume now that Alice doesn’t have to go over the rabbit to catch it, and that she just have to be close enough, in a range $d$ of the rabbit. What is the new formula ?

Let’s consider that the approach is the same (we will try to prove that this is true latter), in this case we can revisit the triangle definition:

  • $\vec{AB}$ is known by definition,
  • $\vec{BC(t)} = t \vec{v_B} $ is dependant of $t$,
  • $AC(t) = t | \vec{v_A} | + d = t . s_A + d $ is a distance dependant of $t$.

And precedant formula becomes:
${(\boldsymbol t . s_A + d)}² = {AB}² + {(\boldsymbol t . s_B)}² + 2 \boldsymbol t . \vec{AB}.\vec{v_B}$

or

$ ({s_B}² - {s_A}²) \boldsymbol t² + 2 ( \vec{AB}.\vec{v_B} - s_A . d ) \boldsymbol t + ({AB}² - d²) = 0 $

Once solved it can be used to derived $C(t)$ (from $\vec{BC(t)}$), which is still the position that reached by the rabbit at $t$. From that position we obtain $\vec{AC}$ the direction in which $A$ should move to reach the point at given range.

see also:

relevant

Written on April 1, 2022, Last update on April 13, 2023
math codingame triangle collision